Question 1 (c)

(c) The zinc-air cell is taken to the top of a mountain where the air pressure is lower. (i) Will the cell potential be higher, lower, or the same as the cell potential at the lower elevation? The cell potential will be lower. 1 point is earned for indicating a lower cell potential. (ii) Justify your answer to part (c)(i) based on the equation for the overall cell reaction and the information above. 02(g), a reactant in the cell reaction, will be at a lower partial pressure at the higher elevation; thus the reaction has a ater value of closer to Deviations in partl pressure t att et e ce closer to equilibrium will decrease the magnitude of the cell potential. 1 point is earned for a justification that relates a lower pressure (or concentration) of 02(g) to Q, or a qualitative approach using e uation.

![In electrochemistry, the Nernst equation is an equation that relates the reduction potential of an electrochemical reaction (half-cell or full cell reaction) to the standard electrode potential, temperature, and activities (often approximated by concentrations) of the chemical species undergoing reduction and oxidation Nernst equation - Wikipedia https://en.wikipedia.org/wiki/Nernst\_equation kT (Redl F [Redl ](./media/image228.png)

The Nernst Equation The effect of concentration on cell emf can be obtained from the effect of concentra- tion on free-energy change. ax: (Section 19.7) Recall that the free-energy change for any chemical reaction, AG, is related to the standard free-energy change for the reac- tion, AGO: AG = AGO + RT1nQ \[20.15\] The quantity Q is the reaction quotient, which has the form of the equilibrium-constant expression except that the concentrations are those that exist in the reaction mixture at ex-x-a (Section 15.6) a given moment. Substituting AG = —nFE (Equation 20.11) into Equation 20.15 gives nFE — -nFEO + RT1nQ Solving this equation for E gives the Nernst equation: In Q This equation is customarily expressed in terms of the base-IO logarithm: 2.303 RT log Q \[20.16\] \[20.17\] At T = 298 K, the quantity 2.303 RT/F equals 0.0592, with units of volts, and so the Nernst equation simplifies to 0.0592 v logQ (T = 298 K) n \[20.18\]

Question 2 (c)

Relationship between AGO and K We can now use Equation 19.19 to derive the relationship between AGO and the equi- librium constant, K. At equilibrium, AG = 0 and Q = K. Thus, at equilibrium, Equa- tion 19.19 transforms as follows: AG = AGO + RT1nQ O = AGO + RT1nK AGO = -RT1nK \[19.20\] Equation 19.20 is a very important one, with broad significance in chemistry. By relating K to AGO, we can also relate K to entropy and enthalpy changes for a reaction.

We can also solve Equation 19.20 for K, to yield an expression that allows us to calculate K if we know the value of AGO: AGO In K -RT -AGO/RT \[19.21\] As usual, we must be careful in our choice of units. In Equations 19.20 and 19.21 we again express AGO in kJ/mol. In the equilibrium-constant expression, we use atmospheres for gas pressures, molarities for solutions; and solids, liquids, and solvents do not appear in the expression. (Section 15.4) Thus, the equi- librium constant is KP for gas-phase reactions and Kc for reactions in solution. Section 15.2 From Equation 19.20 we see that if AGO is negative, In K must be positive, which eans K > 1. Therefore, the more negative AGO is, the larger K is. Conversely, if AGO is ositive, In K is negative, which means K < 1. Finally, if AGO is zero, K = 1.

Question 2 (e)

In a tetrahedral molecular geometry, a central atom is located at the center with four substituents that are located at the comers of a tetrahedron. The bond angles are cos-l(-%) = 109.4712206...0 = 109.50 when all four substituents are the same, as in methane (CH4) as well as its heavier analogues. Tetrahedral molecular geometry - Wikipedia https://en.wikipedia.orgnvikinetrahedral\_molecular\_geometry

Question 2 (f)

(f) During the dehydration experiment, C2H4(g) and unreacted C2H50H(g) passed through the tube into the water. The C2H4 was quantitatively collected as a gas, but the unreacted C2H50H was not. Explain this observation in terms of the intermolecular forces between water and each of the two gases. Ethene is only slightly soluble in water because the weak dipole/induced dipole intermolecular attractions between nonpolar ethene molecules and polar water molecules are weaker than the hydrogen bonds between water molecules. Ethanol molecules are soluble in water because they are polar and form hydrogen bonds with water molecules as they dissolve. I point is earned for comparing of ethene in water with the solubility of ethanol in water in terms of differences In olarit I point is earned for describing the intermolecular forces between ethene and water as weak di ole/induced di ole forces and attributing the solubility o et ano m water to the formed between ethanol molecules and water molecules.

The London dispersion force is the weakest intermolecular force. The London dispersion force is a temporary attractive force that results when the electrons in two adjacent atoms occupy positions that make the atoms form temporary dipoles. This force is sometimes called an induced dipole-induced dipole attraction. London Dispersion Forces https:ffwww.chem.purdue.edu/gchelp/liquids/disperse.html

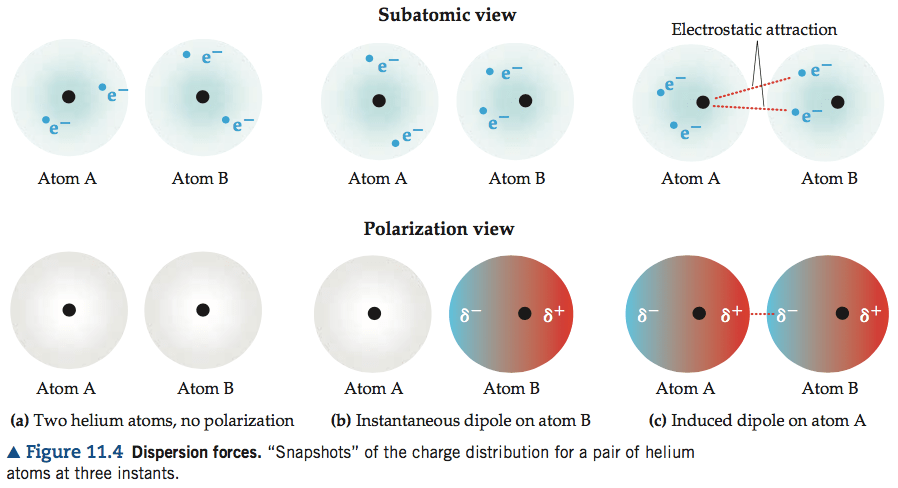
Subatomic view Electrostatic attraction e Atom A e Atom B Atom A Atom A Atom B Atom B Polarization view Atom A Atom B e e Atom A Atom A Atom B Atom B (a) Two helium atonns, no polarization (b) Instantaneous dipole on atom B (c) Induced dipole on atom A A Figure 11.4 Dispersion forces. "Snapshots" of the charge distribution for a pair of helium atoms at three instants.

Question 4 (b)

(b) Calculate the molar solubility of Ca(OH)2 Ksp = \[Ca2+\] \[OH-\]2 1.3 x 10-6 = (0.10 + x) (2x)2 (0.10) 4x2 1.3 x 10-5 = 4x2 x = 0.0018M Molar solubility of = 0.0018 M in 0.10 M \[assuming x << O. 10\] I point is earned for the correct stoichiometry and setup. 1 point is earned for the final answer.

Question 6

  • Anion: A Negative ION

  • CATion: PAWSitive (cats have paws)

    ΙΙΙΚΕΤΟΤΗΙΝΚ ροέιτινει•γ l'MACATlON

Question 7 (a)

(a) Calculate the amount of heat needed to purify 1.00 mole of Al originally at 298 K by melting it. The melting point of Al is 933 K. The molar heat capacity of Al is 24 and the heat of fusion of Al is 10.7 kJ/moI. To raise the temperature from 298 K to 933 K: 24 J x 1.00 mol x 635 15,000 J = 15 kJ mol K It takes 10.7 kJ to melt the Al at 933 K. 5 kJ + 10.7kJ = 26 kJ I point is earned for calculating the amount of heat needed to raise the temperature to 933 K. I point is earned fo addin the heat of fusion to the previous resu t to get a final answer.

results matching ""

    No results matching ""