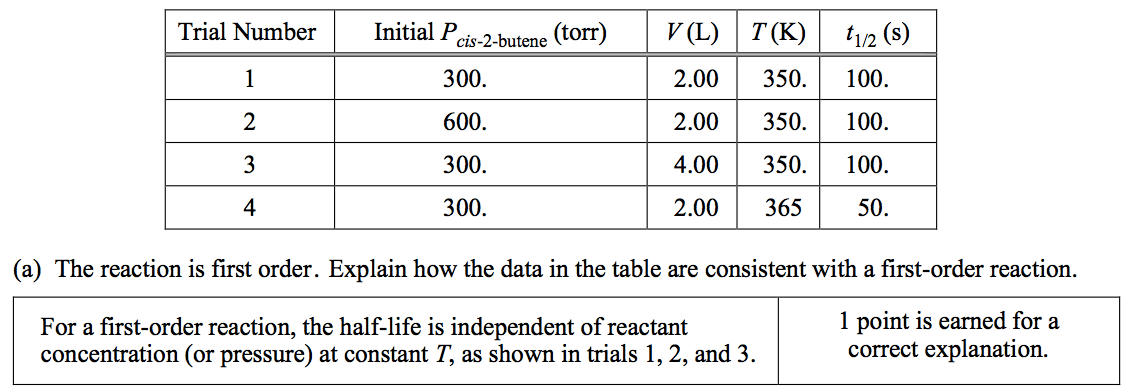
Question 1 (a)

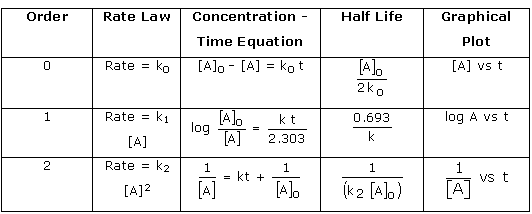
Question 2 (a)
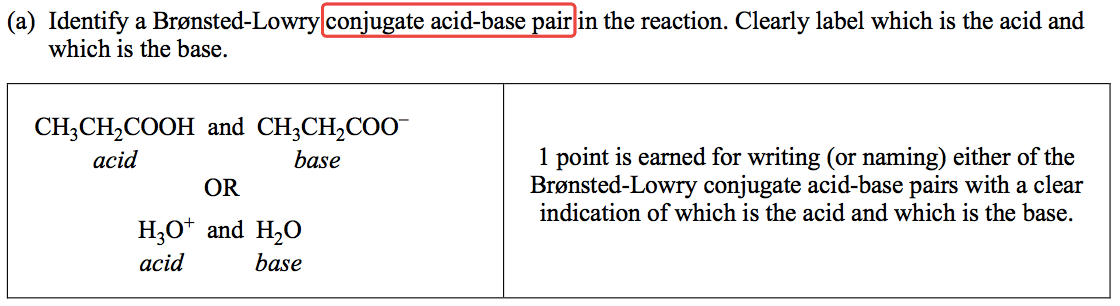
Question 3 (c)
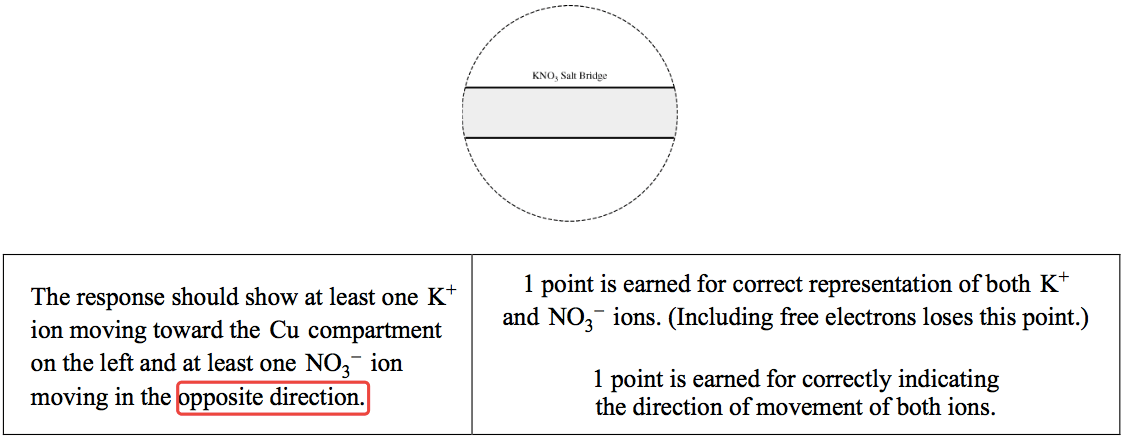
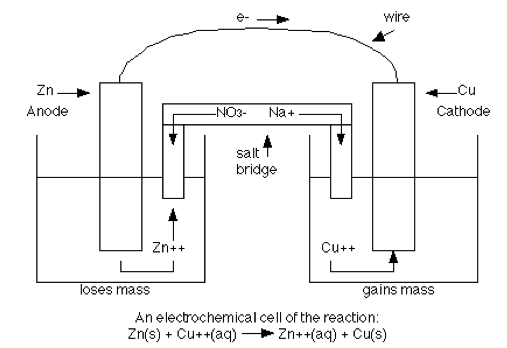

Question 3 (e)
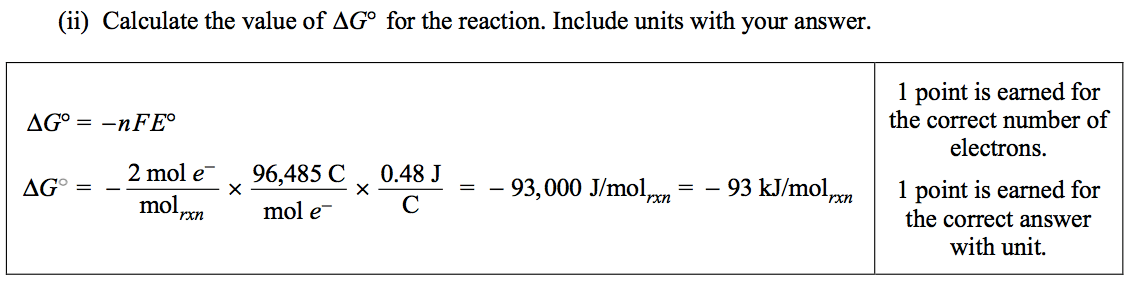

Question 4 (c)

Question 5 (b)

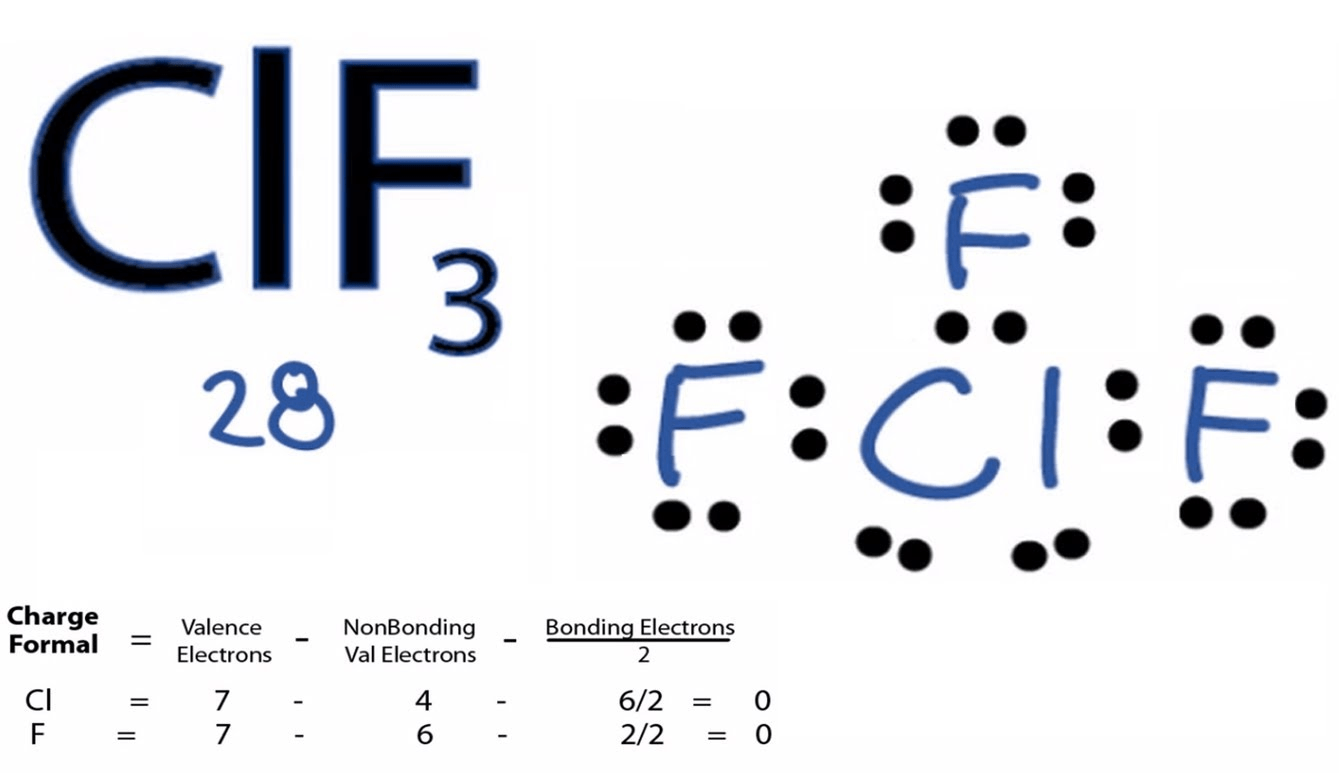
Question 6 (b)
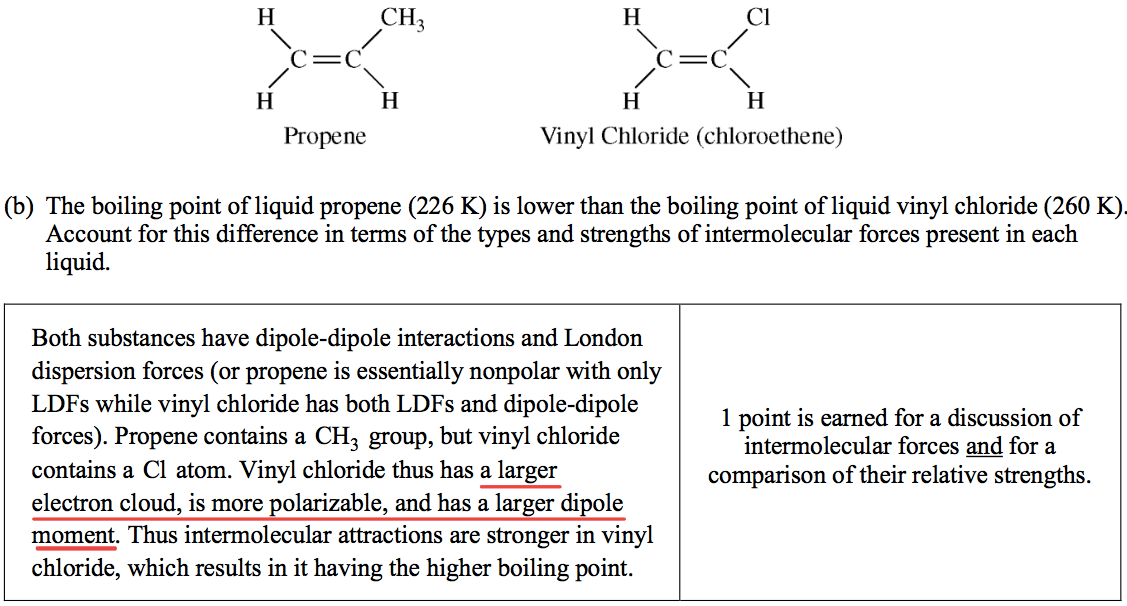
Question 7 (a)
![0.20 0.15 mol 1st half life 0.10 2nd 0.05 half life 0.00 Time, sec
\[A\] vs time for a O order reaction alf life ecrease with decreasin
concentration. 3td half life 20 40 60 80](media/image208.png)
![\[A\] vs time for a 1st order reaction 0.20 engtho hålf life I
constan 4 st half life half life half life 0.00 Time, sec.](media/image209.png)
![\[A\] vs time for a 2nd order reaction 0.20 Length of half life
increases ith decreasing concentration. mol half half life half life
100 200 Time, sec. 300 400](media/image210.png)
![Half-Life The half-life ofa reaction, h n, is the time required for
the concentration ofa reac- tant to reach half its initial value, \[A
h 2 — Half-life is a convenient way to de- scribe how fast a reaction
occurs, especially if it is a first-order process. A fast reaction has
a short half-life. We can determine the half-life of a first-order
reaction by substituting A = —kt1/2 ITC —kt1/2 Time A Figure 14.10
Comparison of first-order and zero-order reactions for the
disappearance of reactant A with time. for CA\] tand t1/2 for t in
Equation 14.12: In — t1/2 = \[14.15\] k 0.693 k From Equation 14.15,
we see that t1/2 for a first-order rate law does not depend on the
initial concentration of any reactant. Consequently, the half-life
remains constant throughout the reaction. If, for example, the
concentration of a reactant is 0.120 M at some instant in the reac-
tion, it will be M) = 0.060 M after one half-life. After one more
half-life passes, the concentration will drop to 0.030 M, and so on.
Equa- tion 14.15 also indicates that, for a first-order reaction, we
can calculate t1/2 if we know k and calculate k if we know t1/2. The
change in concentration over time for the first-order rearrange- ment
of gaseous methyl isonitrile at 199 oc is graphed in Figure 14.11.
Because the concentration of this gas is directly proportional to its
pres- sure during the reaction, we have chosen to plot pressure rather
than concentration in this graph. The first half-life occurs at 13,600
s (3.78 h). At a time 13,600 s later, the methyl isonitrile pressure
(and therefore, 150 75 h/2 37.5 10,000 20,000 Time (s) 30,000
concentration) has decreased to half of one-half, or one-fourth, of
the initial value. In a first-order reaction, the concentration of the
reactant decreases by one-half in each of a series of regularly spaced
time intervals, each interval equal to ti/2. A Figure 14.11 Kinetic
data for the rearrangement of methyl isonitrile to acetonitrile at 199
'C, showing the half-life of the reaction.](media/image211.png)
![The half-life for second-order and other reactions depends on
reactant concentra- tions and therefore changes as the reaction
progresses. We obtained Equation 14.15 for the half-life for a
first-order reaction by substituting \[A h 2 = for \[A)tand ti/2 for t
in Equation 14.12. We find the half-life of a second-oråer reaction by
making the same substitutions into Equation 14.14: \[Alo — \[A\] 0 1 1
— kt1/2 + 2 C A 10 1 = kt1/2 1 \[14.17\] In this case, the half-life
depends on the initial concentration of reactant—the lower the initial
concentration, the longer the half-life.](media/image212.png)
Question 7 (c)
![(c) Is the initial rate of the reaction in trial 1 greater than,
less than, or equal to the initial rate in trial 2 ? Justify your
answer. The initial rate in trial 1 is less than that in trial 2
because rate k \[cis-2-butene\] or rate kP cis-2-butene (with
reference to values from both frials). OR because the initial
concentration of cis-2-butene in trial 1 is less than that in trial 2
and k is constant. 1 point is earned for the correct answer with
justification.](media/image213.png)
Question 7 (d)
